회귀 (Regression)
카테고리: ML
태그: 회귀
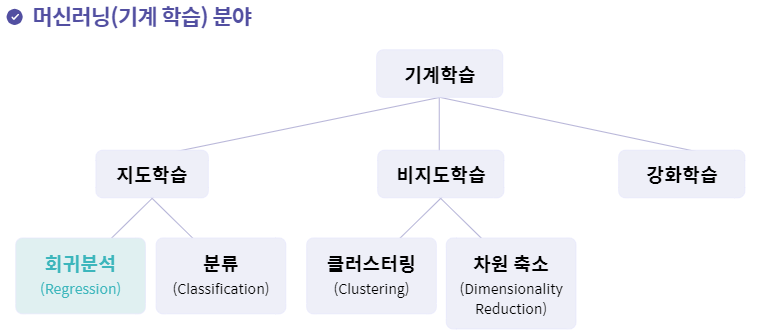
머신러닝 분야
회귀 분석이란?
- 데이터를 가장 잘 설명하는 선을 찾아 입력값에 따른 미래 결과값을 예츧하는 알고리즘
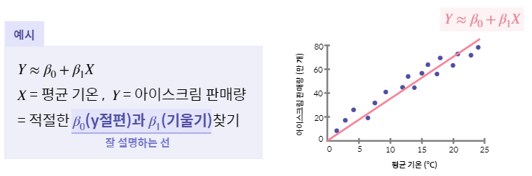
적절한 $\beta_0$(y 절편)과 $\beta_1$(기울기) 찾기
- 완벽한 예측은 불가능!!
- 각 데이터의 실제 값과 모델이 예측하는 값의 **차이를 최소한으로 하는 선을 찾자
- 전체 모델의 차이. 즉, Loss function을 최소로 만드는 $\beta_0, \beta_1$ 구하기
Gradient Descent(경사하강법)
- 최적의 값을 찾기 위한 거꾸로 된 산을 내려가는 방법
- 전체 모델의 차이. 즉, Loss function을 최소로 만든는 $\beta_0, \beta_1$ 을 선정함
💡회귀 분석 개념 정리
Loss Function(실제 값과 모델이 예측하는 값의 오차)를 최소화하는
Gradient Descent(최적의 $\beta_0, \beta_1$를 찾는 알고리즘)을 통해
데이터를 가장 잘 설명할 수 있는 선을 찾는 방법
단순 선형회귀
- 가장 기본적이고 간단한 방법의 회귀 알고리즘
- 입력값 X와 결과값 Y의 관계를 설명할 때 가장 많이 사용되는 단순한 모델
- 데이터를 잘 설명할 수 있는 선을 찾아 새로운 데이터에 대한 결과값 확인 가능 이러한 가장 단순한 회귀 모델을 단순 선형회귀(Simplr Linear Regression)라고 한다.
단순 선형회귀 특징
- 가장 기초적이나 여전히 많이 사용되는 알고리즘
- 입력값(X)이 1개인 경우에만 적용이 가능함
- 입력값과 결과값의 관계를 알아보는데 용의함
- 입력값이 결과값에 열마나 영향을 미치는지 알 수 있음
- 두 변수 간의 관계를 직관적으로 해석하고자 하는 경우 활용
다중 선형회귀(Multiplt Linear Regression)
- 입력값 X가 여러 개(2개 이상)인 경우 활용할 수 있는 회귀 알고리즘
- 각 개별 $X_i$에 해당하는 최적의 $\beta_i$를 찾아야함 \(Y \thickapprox \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_iX_i\)
다중 선형회귀 특징
- 여러 개의 입력값과 결과값 간의 관계 확인 가능
- 어떤 입력값이 결과값에 어떠한 영향을 미치는지 할 수 있음
- 여러 개의 입력값 사이 간의 상관 관계가 높을 경우 결과에 대한 신뢰성을 잃을 가능성이 있음
다항 회귀(Polynomial Regression)
- 1차 함수 선형식으로 표현하기 어려운 분포의 데이터를 위한 회귀
- 복잡한 분포의 데이터의 경우 일반 선형 회귀 알고리즘 적용 시 낮은 성능의 결과가 도출됨
- 데이터의 분포에 더 잘 맞는 모델이 필요함 \(Y \thickapprox \beta_0 + \beta_1X_1 + \beta_2X^2_2 + \cdots + \beta_iX_i^i\)
다항 회귀 원리
-
기존 입력값 $X_i$를 전처리 한 새로운 변수를 추가시켜 선형 회귀 모델로 예측할 수 있도록 함 \(Y \thickapprox \beta_0 + \beta_1X_1 + \beta_2X_2^2\)
-
- 사실은 다중 선형 회귀와 동일한 원리
- \(Y \thickapprox \beta_0 + \beta_1X_1 + \beta_2X_2\)
- 각 개별 입력값 $X_i$에 해당하는 최적의 \beta_i를 찾아야 함
다항 회귀 특징
- 일차 함수 식으로 표현할 수 없는 복잡한 데이터 분포에도 적용 가능
- 극단적으로 높은 차수의 모델을 구현할 경우 과도하게 학습 데이터에 맞춰지는 과적합 현상 발생
- 데이터 관계를 선형으로 표현하기 어려운 경우 사용
과적합
- 모델이 주어진 훈련 데이터에 과도하게 맞춰져 새로운 데이터가 입력 되었을 때 잘 예측하기 못하는 현상
- 즉, 모델이 과도하게 복잡해져 일반성이 떨어진 경우를 의미함
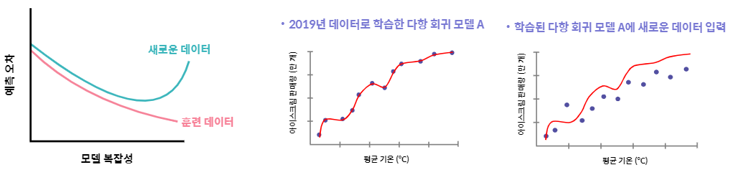
과적합 방지 방법
- 모델이 잘 적합되어 실제 데이터와 유사한 에측 결과를 얻을 수 있도록 과적합 방지를 위해 다양한 방지를 다양한 방법을 사용함
=> 교차 검증(Cross Validation), 정규화(Regularization)
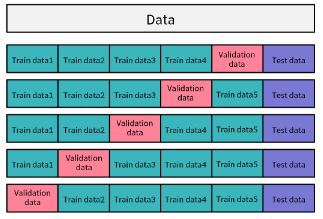
교차 검증(Cross Validation)
- 모델이 잘 적합되었는지 알아보기 위해 훈련용 데이터와 별개의 테스트 데이터, 그리고 검증 데이터로 나누어 성능 평가하는 방법
- 다양한 방법들이 있지만, 일반적으로 K-fold 교차 검증을 많이 사용함

K-fold 교차 검증
- 훈련 데이터를 계속 변경하여 모델을 훈련시킴
: 데이터를 K등분으로 나누고 K번 훈련시킴
- K를 설정하여 데이터 셋을 K개로 나눔
- K개 중 한 개를 검증용, 나머지를 훈련용으로 사용
- K개 모델의 평균 성능이 최종 모델 성능
정규화(Regularization)
-
- 모델의 복잡성을 줄여 일반화된 모델 구현을 위한 방법
- -> 모델 $\beta_i$에 패널티를 부여함
- 선형 회귀를 위한 정규화: L1, L2 정규화
선형 회귀를 위한 정규화 방법
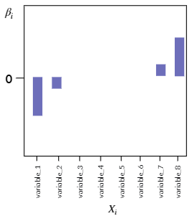
L1 정규화(Lasso)
- 불필요한 입력값에 대응되는 $\beta_i$를 정확히 0으로 만든다.
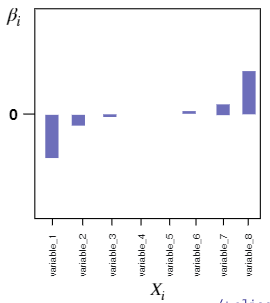
L2 정규화(Ridge)
- 아주 큰 값이나 작은 값을 가지는 이상치에 대한 $\beta_i$를 0에 가까운 값으로 만든다.
정규화를 적용한 회귀
Lasso Regression
- 회귀 학습에 사용되는 Loss Function(비용 함수)에 L1 정규화 항을 추가
- 중요하지 않는 $\beta_i$를 0으로 만들어 모델의 복잡성을 줄일 수 있음
Lasso Regression 특징
- 너무 많은 $\beta_i$를 0으로 만들 수 있어 모델의 정확성이 떨어질 수 있음
- 몇 개의 중요 변수만 선택하기 때문에 정보 손실의 가능성이 있음
Ridge Regression
- 회귀 학습에 사용되는 Loss Function(비용 함수)에 L2 정규화 항을 추가
- 중요하지 않은 $\beta_i$를 0에 가깝게 만들어 모델의 복잡성을 줄일 수 있음
Ridge Regrssion 특징
- $\beta_i$를 0에 가깝게 만들지만 완전한 0은 아니기 때문에 모델이 여전히 복잡할 수 있음
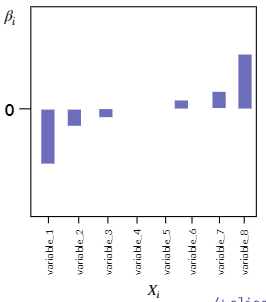
Elastic Net Regression
- Lasso 회귀, Ridge 회귀의 단점을 보완하기 위함
- Lasso 회귀의 L1 정규화와 Ridge 회귀의 L2 정규화 적용 비율을 조정하여 모델을 구현
회귀 알고리즘 평가 지표
- 어떤 모델이 목표를 얼마나 잘 달성했는지 정도를 평가해야 함
- 과대적합의 반대의미로, 모델이 너무 단순하여 학습된 데이터조차 잘 예측하지 못하는 현상을 잡는다.
목표 달성 평가 방법
- 실제 값과 모델이 예측하는 값의 차이에 기반한 평가 방법 사용
ex) RSS, MSE, MAE, MAPE, $R^2$
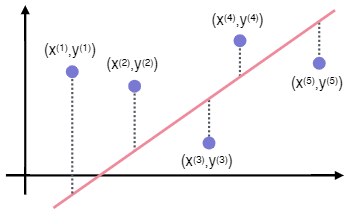
RSS(Residual Sum of Squares) - 단순 오차
- 실제값과 예측값의 단순 오차 제곱 합
- 값이 작을수록 모델의 성능이 높음
- 전체 데이터에 대한 실제 값과 예측하는 값의 오차 제곱의 총합
RSS 특징
- 가장 간단한 평가 방법으로 직관적인 해석이 가능함
- 그러나 오차를 그대로 이용하기 때문에 입력값의 크기에 의존적임
MSE, MAE - 절대적인 크기에 의존한 지표
MSE(Mean Squared Error)
- 평균 제곱 오차, RSS에서 데이터 수만큼 나눈 값
- 작을수록 모델의 성능이 높다고 평가할 수 있음
MAE(Mean Absolute Error)
- 평균 절대값 오차, 실제값과 예측값의 오차의 절대값의 평균
- 작을수록 모델의 성능이 높다고 평가할 수 있음
MSE, MAE 특징
- MSE: 이상치(Outlier). 즉, 데이터들 중 크게 떨어진 값에 민감함
- MAE: 변동성이 큰 지표와 낮은 지표를 같이 예측할 시 유용
- 가장 간단한 평가 방법들로 직관적인 해석이 가능함
- 그러나 평균을 그대로 이용하기 때문에 입력값의 크기에 의존적임
$R^2$ (결정 계수)
- 회귀 모델의 설명력을 표현하는 지표
- 1에 가까울수록 높은 성능의 모델이라고 해석할 수 있음 \(1 - {SSE \over TSS}(0 \leq R^2 \leq 1)\)
$R^2$ 특징
- 백분율로 표현하기 때문에 크기에 의존적이지 않음
- 실제값이 1보다 작을 경우, 무한대에 가까운 값 도출, 실제값이 0일 경우엔 계산 불가
🔥절대적인 평가 지표는 존재하지 않음!
다양한 평가 지표를 적용해보고, 결과값을 비교하며 모델의 성능을 다양한 측면에서 확인해봐야 함

댓글 남기기